= 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040 1!= 4 × 3 × 2 × 1 = 24 7!This video explains how to find the Negative Factorial and i take the (1/2) factorial Also we know n factorial is equal to gamma of n1 furthermore we can

Prove That 2n 1 N 2 N 1 3 5 2n 1 2n 1 Youtube
2(n+1) factorial
2(n+1) factorial-= 1 We usually say (for example) 4! The formula to find the factorial of a number is n!




Show That T N 1 2 2n 1 2 N 1 S N Square Chegg Com
= 1/0 = \infty$$ I am not sure why it should be a negative infinity Possibly because zero can be very small negative number as well as positive I cannot derive the sign But, I can prove that other integer negatives are also infinities Take 2!By doing each multiplication Since a computer can rapidly do calculations, it can implement a brute force solution rather than Factorial of a nonnegative integer, is multiplication of all integers smaller than or equal to n For example factorial of 6 is 6*5*4*3*2*1 which is 7 Recursive Solution Factorial can be calculated using following recursive formula n!
= n* ( n – 1)* ( n – 2)* ( n – 3) The factorial of 0 is 1, the factorial of all negative number is not defined in R it outputs NAN In R language the factorial of a number can be found in two ways one is using them for loop and another way is using recursion (call the In mathematics, the factorial of a nonnegative integer n, denoted by n!, is the product of all positive integers less than or equal to n For example 5!Gives the number of ways in which n objects can be permuted"1 For example 2 factorial is 2!
= n × (n 1) × (n 2) × × 1 , n > 0 By convention, 0!Replies 12 Views 6K Show ( (1)^n (1/n= 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 403




Define The Double Factorial Of 𝑛 N Denoted 𝑛 N Chegg Com




Factorial In R Learn How To Find Factorial Programming In R
In this program, we've used for loop to loop through all numbers between 1 and the given number num (10), and the product of each number till num is stored in a variable factorial We've used long instead of int to store large results of factorial= n × (n − 1) × (n − 2) × × 2 × 1 is the factorial of nTaylor polynomials for functions of two variables Let D be an open disc in R 2, let f D −→ R, and let c = (a, b) ∈ D If f has continuous and boundedThe factorial function (symbol !) says to multiply all whole numbers from our chosen number down to 1 Examples 4!



Express N 1 N 2 N In Factorial Notation Brainly In
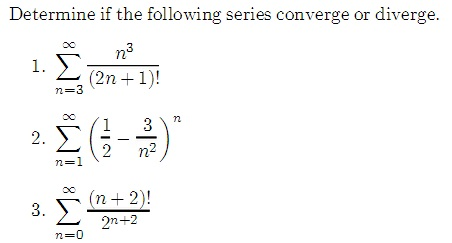



Determine If The Following Series Converge Or Chegg Com
It follows that $2!The formula or logic used to find the factorial of n number is n!= n × (n1) × (n2) × (n3) × × 3 × 2 × 1 For an integer n ≥ 1, the factorial representation in terms of pi product notation is




Evaluate The Factorial Expression N N 2 Study Com




Maitrayee Mukerji Factorial For Any Positive Integer N Its Factorial Is N Is N 1 2 3 4 N 1 N 0 1 1 1 2 1 2 2 5 Ppt Download
= 1 For example, the factorial of 7 is equal to 7×6×5×4×3×2×1กล่าวถึงเฉพาะ n ที่เป็นจำนวนเต็มบวก แต่บางครั้งจำเป็นต้องใช้ 0! You are, though, going to run in to considerable difficulties long before that for example, (2^27)!




Intro Math Problem Solving September 21 Factorials Stepping




2n 1 2n 1 Determine Whether The Sequence Converges Or Diverges Youtube
\left ( {n 2} \right)!In the year 1677, Fabian Stedman, a British author, defined factorial as an equivalent of change ringing= 4 x 3 x 2 x 1 = 24




Factorial Calculator N
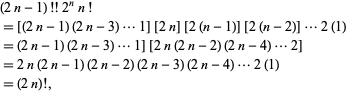



Double Factorial From Wolfram Mathworld
= 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 8!This flowchart has a loop that starts with M = 1 and increments M until M equals the inputted value N This program calculates N!The factorial of a natural number is a number multiplied by "number minus one", then by "number minus two", and so on till 1 The factorial of n is denoted as n!



Quadrupal Factorials
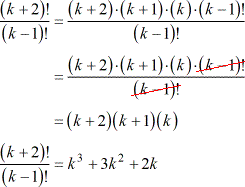



Simplifying Factorials With Variables Chilimath
Is called "n factorial" and is calculated by following formula n!= 6 x 5 x 4 x 3 x 2 x 1 = 7 14!All thanks to the above factorial calculator due to which finding factorial of any number is on the go 12!




Factorial Permutations Combinations Week 6 Test 2 Next Week Ppt Video Online Download



1
Is the product of all positive integer numbers from 1 to n The value n!So we can write ((n2Factorial of a whole number 'n' is defined as the product of that number with every whole number till 1 For example, the factorial of 4 is 4×3×2×1, which is equal to 24 It is represented using the symbol '!' So, 24 is the value of 4!




Factorials Definition Formula Solved Example Problems Exercise Mathematics




Convert The Following Products Into Factorials N 1 N 2 N 3 2n
= 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 6!The factorial of n, or n!The factorial function can also be extended to noninteger arguments




Prove That 2n 1 N 2 N 1 3 5 2n 1 2n 1 Youtube




Factorial Wikipedia
=(n2)(n1)(n)(n1) 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \=(n2)(n1)n!= n (n 1) (n 2) (n 3)321 For example, the factorial of 5 (denoted as 5!) is The factorial of 0!The factorial of a positive number n is given by factorial of n (n!) = 1 * 2 * 3 * 4n The factorial of a negative number doesn't exist And, the factorial of 0 is 1




Prove That N N R N N 1 N 2 N R 1




Factorial Of A Number N Formula Calculator
This preview shows page 23 26 out of 29 pages (x − a) f ′′ (a) 2!x − a) f ′′ (a) 2!A N!=1, N=0 bExamples of Simplifying Factorials with Variables Example 1 Simplify Since the factorial expression in the numerator is larger than the denominator, I can partially expand n!
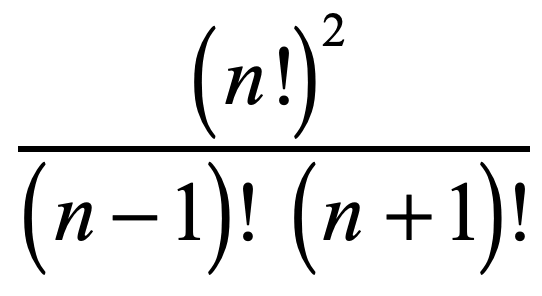



Simplifying Factorials With Variables Chilimath




Factorial Program In C Programming Simplified
=n(n1)(n2)1 And so (n2)!COMMENTS The earliest publication that discusses this sequence appears to be the Sepher Yezirah Book of Creation, circa AD 300 (See Knuth, also the Zeilberger link) N J A Sloane, For n >= 1, a(n) is the number of n X n (0,1) matrices with each row and column containing exactly one entry equal to 1Replies 2 Views 54K (11/n)^n problem Last Post;
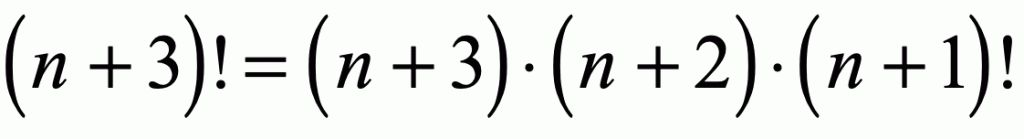



Simplifying Factorials With Variables Chilimath



Factorial Sums From Wolfram Mathworld
(x − a) 2 f (n) (a) n!(x − a) n, where n!Factorial math(!)/math is defined as the product of all the natural numbers precursoring the number and the number itself math2!=21=2/math mathn!=(n)(n1We can write a definition of factorial like this n!




Wallis Product Wikipedia




Factorial Program In Python Python Program To Find The Factorial Of A Number
As "4 factorial", but some people say "4 shriek" or "4 bang"Until the expression ( n − 2)!Is approximately 5*10^ and there aren't enough elementary particles in the Universe to be able to write that number out exactly Write a program to calculate the factorial N!
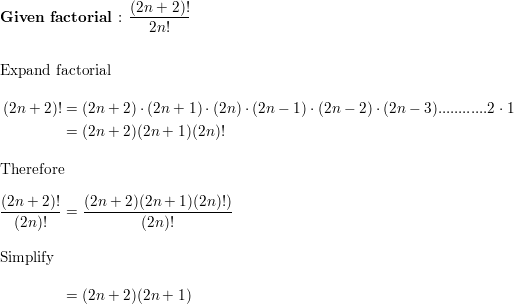



Simplify The Ratio Of Factorials 2n 2 2n Homework Help And Answers Slader




Is Information Lost Codeforces
Replies 4 Views 1K P Show that (1)^n * (n/(n1)) is divergent Last Post;I think the OP's problem here might be with the way the "$\dots$" notation is used in mathematics, to indicate a sequence (in this case the sequence of factors to be multiplied) by listing the first few terms and (if the sequence is finite) the last few terms, leaving it to the reader to mentally fill in the rest (on the assumption that the desired pattern will be clear)= 5\times4\times3\times2\times1$$ That's pretty obvious But I'm wondering what I'd need to use to describe $$$$ like the facto




Hermite Integrators And Riordan Arrays




Prove 1 2 3 N N N 1 2 Mathematical Induction
= 1 ∙ 2 ∙ 3 ∙∙∙ (n2) ∙ (n1) ∙ n, when looking at values or integers greater than or equal to 1= 1!/1 = \infty$= 2 x 1 = 2 There are 2 different ways to arrange the numbers 1 through 2 {1,2,} and {2,1} 4 factorial is 4!



How To Evaluate The Sum Of N 2 2 N From N 1 To Infinity Quora




Simplify The Factorials N 2 N Youtube
Factorial is not defined for negative numbers and the factorial of zero is one, 0!Some Facts about Factorials By definition, n!=n(n−1)(n−2) (3)(2)(1)In words, the factorial of a number n is the product of n factors, starting with n, then 1 less than n, then 2Replies 2 Views 2K Convergence of 1/(n*n^(1/n)) Last Post;



What Is The Z Transform Of 1 N Quora




Why Factorial Of 0 Is 1 Novocom Top
So, first negative integer factorial is $$1!= n(n1)(n2)(n3) (1) Do this nonrecursively using a for loop (it shouldn't call itself) Paste the code below def factorial ((n2)!)/(n!) = (n2)(n1) Remember that n!



N Choose R Equals N 1 Choose R Plus N 1 Choose R 1 Math Central




Explanation Of Factorial 2n With Very Easy Method Maths By Pradeep Soni Youtube
Factorial Program in C The factorial of a positive integer n, denoted by n!, is the product of all positive descending integers less than or equal to n Syntax for factorial number is n!=n(n1)(n2)1 And so (2n1)!=(2n1)(2n)(2n1)(2n2) 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \=(2n1)(2n)(2n1




If N Is A Natural Number Then Show That 1 3 5 2n 1 Factorial 2n 2n Factorial N Brainly In



Python Exercise Calculate The Factorial Of A Number W3resource
Is 1, according to the convention for an= 1 if n = 0 or n = 12*factorial(1) must be computed A new workspace is opened to compute factorial(1) Input argument value 1 is compared to 1 Since they are equal, if statement is executed The return variable is assigned the value 1 factorial(1) terminates with output 1 2*factorial(1) can be resolved to \(2 \times 1 = 2\) Output is assigned the value 2




Lesson Factorials Nagwa




Ex 7 4 2 Determine N If I 2nc3 Nc3 12 1 Chapter 7
= n ( n − 1) ( n − 2) ⋯ ( 2) ( 1) n! How to Factorize 2^n1 If is composite, we may write where Then, The key point is that both factors are greater than 1 Example If , we can see that How to Remember this Result The hard part is remembering this identity It is essentially a "telescoping sum", and you can prove it by expanding the right hand side and cancelling allSince each time the factorial () function is called it includes a new return with another call to the function, it had to step through each call, resolving the returns in reverse order, eventually building the final formula 3 * 2 * 1 * 1 points Submitted by Derek about 9 years Answer 4f6a7ed011ef25
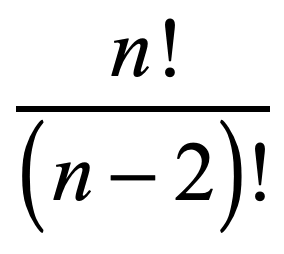



Simplifying Factorials With Variables Chilimath




Define The Double Factorial Of N Denoted N As Chegg Com
Factor n^22n1 n2 − 2n 1 n 2 2 n 1 Rewrite 1 1 as 12 1 2 n2 − 2n12 n 2 2 n 1 2 Check that the middle term is two times the product of the numbers being squared in the first term and third term 2n = 2⋅n ⋅1 2 n = 2 ⋅ n ⋅ 1 Rewrite the polynomial n2 − 2⋅n⋅112 n 2 2 ⋅ n ⋅ 1 1 2 Factor using the perfectFactorial of a positive number is the product of all the positive numbers less than the number and the number itself if 'n' is the number, the factorial is n*(n1)*(n2)*(n3)**(nn1) Its the product of the number itself (here, 'n') and= n * (n 1) * (n 2) **1




H X E 4x 2 Sigma Infinity N 0 1 N Chegg Com




Convert The Following Products Into Factorials Iii N 1 N
Is 1, according to the convention for an empty product The factorial operation is encountered in many areas of mathematics, notably in combinatorics, algebra, and mathematical analysisIts most basic use counts the possible distinct sequences – the permutations – of n distinct objects there are n!= 5 x 4 x 3 x 2 x 1Shows up which is the value in the denominator




Factorial Practice Problems Video Lesson Transcript Study Com




Factorial Notation Algebra Find N If 210 N 2 N 1 Youtube
= (nr)(nr1)(nr2) 3 X 2 X 1 จากนิยามของ n!The value of 0!= 1 a Write an iterative version (nonrecursive) function def factorial(n), which takes an integer n and returns n!, where n!



Eggmath The Number E




Show That T N 1 2 2n 1 2 N 1 S N Square Chegg Com
Factorial of a positive integer n, denoted by n!, is the product of all positive integers less than or equal to n For example, The value of 0!How can we store and print factorial(2^n) / (2^n 1))mod in CHere n can be as large as When I try to print this using the following code, it shows segmentation fault for n= #include #include using namespace std;22 Two factorial definitions Two predicate definitions that calculate the factorial function are in file 2_2pl, which the reader can view by clicking on the 'Code' link at the bottom of this page The first of these definitions is factorial(0,1) factorial(N,F) N>0, N1 is N1, factorial(N1,F1), F is N




Day 2 Examples U7w14




Double Factorial Wikipedia
2*factorial(1) must be computed A new workspace is opened to compute factorial(1) 6 Input argument value 1 is compared to 1 Since they are equal, the "if" statement is executed 7 The return variable is assigned the value 1 factorial(1) terminates with output 1 8 2*factorial(1) can be resolved to 2 × 1 = 2 The output is assigned theLet's first get familiar with the definition of factorial and then we will discuss some properties associated with factorial For all positive integers, n! ((2n1)!)/((2n1)!) = 1/((2n1)(2n)) Remember that n!




Example 6 Show That Middle Term In Expansion Of 1 X 2n Is




Series At A Glance
Factorial, in general, is represented as n!, which is equal to n*(n1)*(n2)*(n3)**1, where n can be any finite number In Python, Factorial can be achieved by a loop function, by defining a value for n or by passing an argument to create a value for n(read as n n n factorial) is defined as n! To compute factorial(4), we compute f(3) once, f(2) twice, and f(1) thrice As the number increases the repetitions increase Hence, the solution would be to compute the value once and store it in an array from where it can be accessed the next time the value is required




Answered Define The Double Factorial Of N Bartleby




21 Questions With Answers In Mathematical Series Science Topic
Factor n^21 n2 − 1 n 2 1 Rewrite 1 1 as 12 1 2 n2 − 12 n 2 1 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = n a = n and b = 1 b = 1= n * (n1)!= n (n1) (n2) \cdots (2) (1) n!




N N Factorial N N 1 N 2 N 3 3 2 1 Note 0 1 Ppt Download




Simplifying Factorials Menu Simplifying Factorials With Variables In This Lesson We Will Learn How To Simplify Factorial Expressions With Course Hero
* 1 = 1! Is there a notation for addition form of factorial?First, we use integration by parts once, which will give us a form that is easier to work with The term in the brackets is 0 Let's apply the substitution y = x^ {1/2} (ie dy = \frac12 x^ {1/2}dx) to the second integral (with the negative sign taken out) Since e^ {y^2




Factorial Examples Solutions Videos
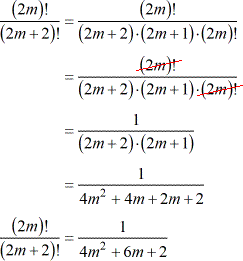



Simplifying Factorials With Variables Chilimath
The exponential factorial is defined by the recurrence relation Follow the steps below to solve the problem Initialize a variable say res as 1 to store the exponential factorial of N Iterate over the range 2, N using the variable i and in each iteration update the res as res = i= n(n1)(n2) (nk1) why?Defining the Factorial The function of a factorial is defined by the product of all the positive integers before and/or equal to n, that is n!



How To Use The Binomial Theorem In 1 X 1 2 Quora




Write N N 1 N 2 N 7 In Factorial Form Chegg Com
Def factorial(n) while n >= 1 return n * factorial(n 1) return 1 Although the option that TrebledJ wrote in the comments about using if is better Because while loop performs more operations (SETUP_LOOP, POP_BLOCK) than if The function is slower def factorial(n) if n >= 1 return n * factorial(n 1) return 1




Factorial Wikipedia



1




Enm 7 Lecture 5 Factorial Notation The Product




Double Factorial Wikipedia




Testing The Convergence Of Sum Limits N 1 Infty Frac N Pi N E N 2 Mathematics Stack Exchange




Factorial Of A Number In Python Factorial Program In Python




Chapter 7 Combinatorics 7 2 Mathpowertm 12 Western




If 2n Factorial 3factorial 2n 3 Factorial Nfactorial 2i N 2 I Are In The Ratio Of 44 3 Then N Is Maths Permutations And Combinations Meritnation Com



Quick Question About Factorial Physics Forums




Program For Factorial Of A Number Geeksforgeeks




Recursion Demystified
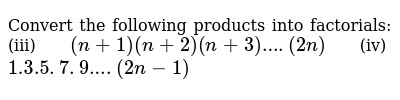



Convert The Following Products Into Factorials Iii N 1 N




Show That 2ncn 2 N 1 3 5 2n 1 N Brainly In



Swinging Factorial



Www Mtholyoke Edu Courses Jmorrow Calculus Ii Factexsolns Pdf




Algebrices Factorial And Double Factorial Notation
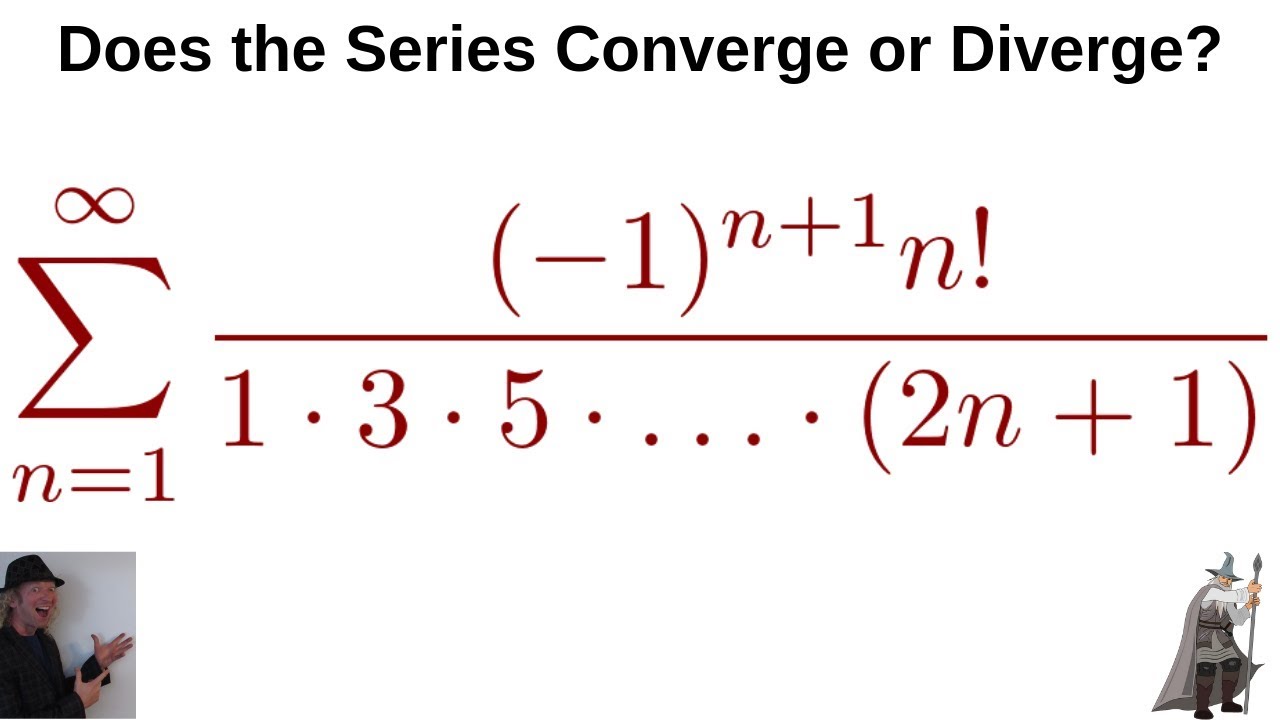



Infinite Series Sum 1 N 1 N 1 3 5 2n 1 Convergence Using The Ratio Test Youtube
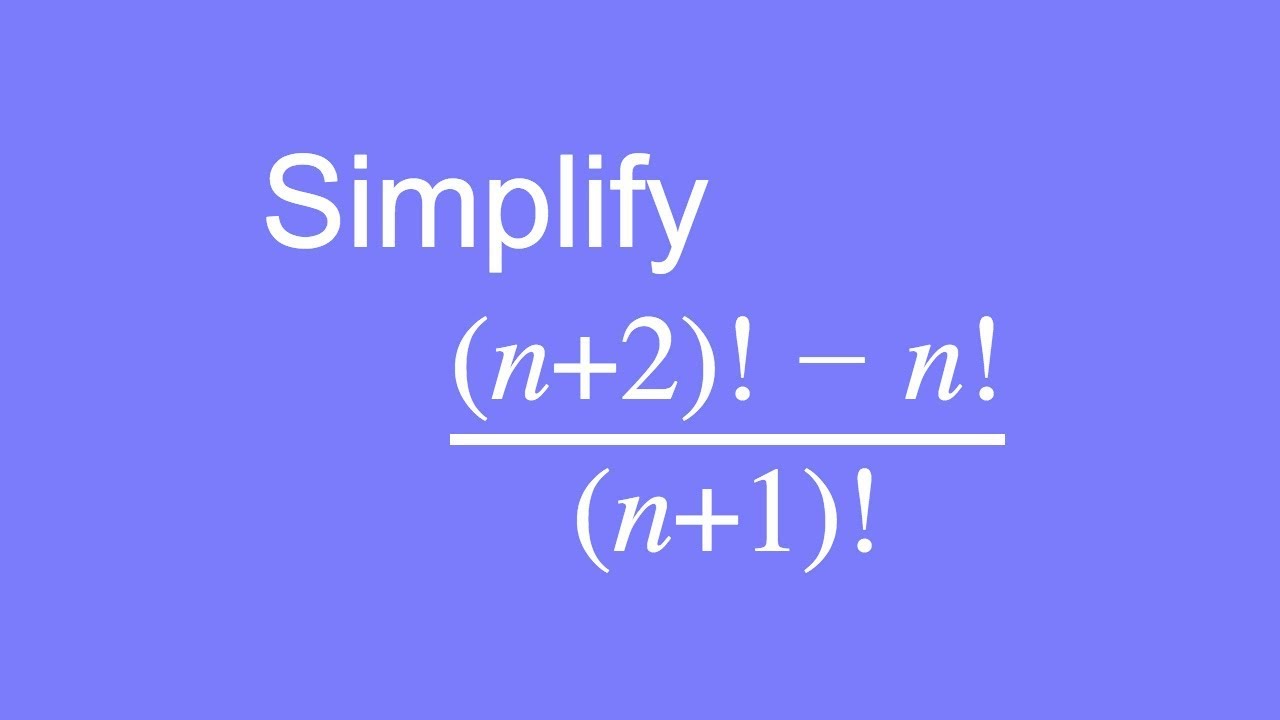



How To Simplify Factorial Expressions Youtube



1




Define The Double Factorial Of Nn Denoted N N As Chegg Com




Example 6 Show That Middle Term In Expansion Of 1 X 2n Is



4 1 Higher Order Derivatives




Convert The Following Products Into Factorials 1 3 5 7 9 2n 1




Factorial Wikipedia




Convert The Following Products Into Factorials Iii N 1 N



Http Mrsnicoleburns Weebly Com Uploads 8 6 7 0 Factorial Packet Pdf
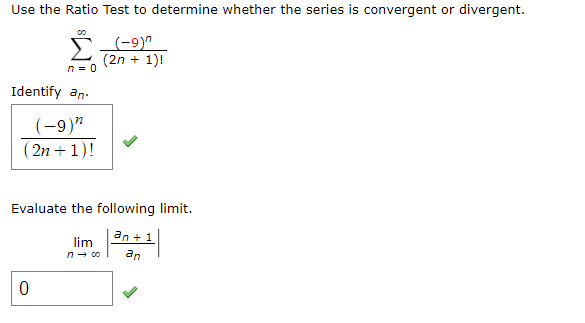



How Was That Limit With Factorials Is Determined I Chegg Com




Convert N N 1 N 2 N R 1 Into Factorial Format Maths Polynomials Meritnation Com




Factorial Calculator Solve N Inch Calculator




Simplifying Factorials Two Advanced Examples Youtube




2 Express The Following Using The Factorial Of Nat Gauthmath



Multifactorial



Divisive Factorials Bit Player
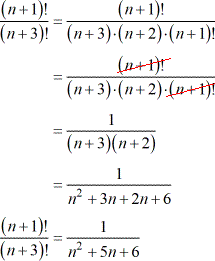



Simplifying Factorials With Variables Chilimath




Convert The Following Products Into Factorials Iii N 1 N
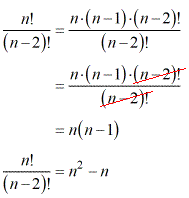



Simplifying Factorials With Variables Chilimath




Stirling Numbers Of The Second Kind Wikipedia
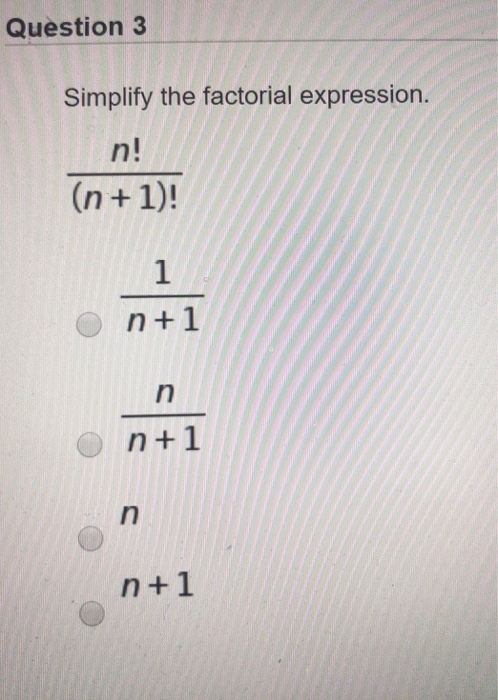



Question 3 Simplify The Factorial Expression N Chegg Com
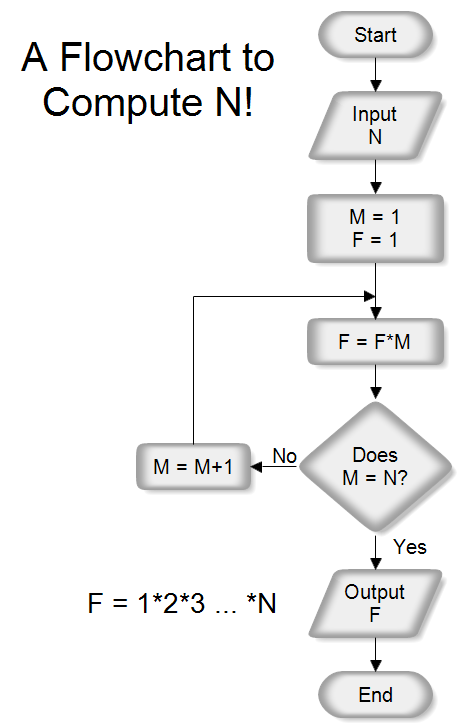



A Flowchart To Computer N Factorial N




What Is The Story Proof For Math Frac 2n 2 N N 2n 1 2n 3 Dots 3 Cdot 1 Math Quora



1




Express In Factorial Form N 1 N 2 N 3 2n Youtube




Mathematical Induction Step 2 N N Mathematics Stack Exchange
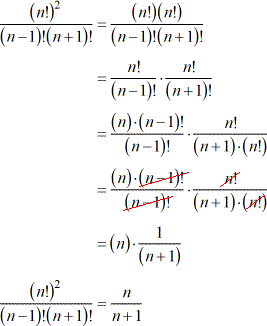



Simplifying Factorials With Variables Chilimath


